Lecții de TIC si INFORMATICĂ : [Liste / stive/cozi/ grafuri /arbori]

Lista

este o structură de date în care elementele sunt de același tip , orice element mai puțin primul are un predecesor și orice element mai puțin ultimul are un succesor.

Sunt cunoscute ca modele de liste lista liniară , lista circulară și lista cu priorități.

Se modelează adesea prin vectori , uneori prin vectori de înregistrări etc

LISTELE PERMIT INSERAREA SAU STERGEREA DE INFORMATIE ÎN ORICE LOC AL SĂU .

Listele de mai sus au fost completate diferit .

Listele pot fi liniare (ca cele de mai sus ) SAU circulare ( ca cea de mai jos )

Observăm că la o listă circulară primul și ultimul element coincid .

Operațiile cu liste sunt : inserarea de noi elemente (push) , ștergerea de elemente (pop) , listarea , căutarea .

Aceste operații sunt folosite și de programele de gestionare a bazelor de date . Bazele de date pot fi modelate și pe baza unor structuri de tip listă .

Reprezentarea conexiunilor dintre elemente se poate face uzual prin lista simplu înlănțuită ( pe care o avem mai sus) sau prin lista dublu înlănțuită( mai jos ) .

Elementele pot fi numite și noduri .

Stiva

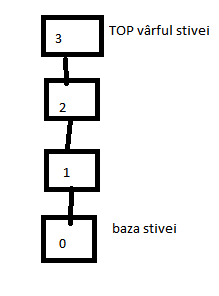
este un caz particular de listă la care operațiile de introducere si extragere de elemente se fac numai printr-un singur capat- varful stivei .

Utilizare majoră - stiva sistem , HEAP-ul în programe C++ cu variabile dinamice , stiva de apeluri recursive de functii . De pildă la un apel al functiei recursive a lui Fibonacci pentru n=5 avem o stivă care are 15 apeluri recursive .

Mai jos vom ilustra o stiva in alocare dinamica . Retinem ca se initializeaza stiva , primul element in stiva este practic si ultimul , se retin doi pointeri relevanti : baza si varful stivei top.

Baza si varful coincid numai daca stiva are un singur element .
Avem introducerea de elemente in stiva , cautarea , tema extragerea de elemente din stiva .

#include <iostream>
#include<conio.h>
#include<stdio.h>
using namespace std;
struct nod{int inf;nod* urm;} ;
int main()
{int key,n,i,info; nod *stiva,*p,*top,*baza;
printf("dati numarul de elemente al stivei n=");scanf("%d",&n);
printf("dati informatia din primul nod info=");scanf("%d",&info);
top=NULL;baza=NULL; //initializarea
p=new nod; p->inf=info; p->urm=NULL;
baza=p; top=p;//varful si baza coincid in stiva cu un singur element
for(i=2;i<=n;i++)
{printf("dati informatia din nod %d =",info);scanf("%d",&info);
p=new nod;
p->inf=info;
p->urm=top;
top=p;
}//listam mai jos stiva
stiva=top;
printf("sunt listate incepand cu vf stivei si avand jos baza ..") ;
do
{
printf("\n %d ",top->inf);
top=top->urm;

} while(top!=NULL);
cout<<"se cere cheia de cautare ";cin>>key;
while(stiva!=NULL)
{ if (key==stiva->inf) cout<<" cheia de cautare a fost gasita ";
stiva=stiva->urm;}
return 0;

}

INDICATIE PT TEMA :

se extrage practic informatia din varful TOP , si ca urmare noul varf al stivei top=top->next, adica noul varf al stivei devine predecesorul varfului curent .
tema 2 la stiva in alocare dinamica :daca ar fi sa inserati o instructiune delete pt a sterge o variabila dinamica unde ati plasa aceasta instructiune ? Mentionati randul in tema .

STIVA IN ALOCARE STATICA

#include <iostream>
using namespace std;
int stack[100],top,baza,n,i,j,info,key;
int main()
{
cout << "crearea stivei" << endl;
top=-1;baza=-1;//conventie pt a spune ca nu avem nimic inca in stiva
cout<<"nr de elemente in stiva = "; cin>>n;
for(i=0;i<n;i++) {
cout<<"informatia utila= "; cin>>info;
if(top==-1) {baza=0;top=0;stack[top]=info;}
else {top++;stack[top]=info;}
}
//listarea
cout<<"LISTARE in ordine inversa introducerii in stiva "<<endl;
for(i=n-1;i>-1;i--) cout<<stack[i]<<endl;
cout<<" cautarea in stiva ";cout<<"key= "; cin>>key;
for(i=n-1;i>-1;i--)if(stack[i]==key)cout<<"cheia de cautare e gasita pe pozitia "<<i<<endl;
cout<<"extragerea din stiva ";
cout<<stack[top]<<endl;
return 0;
}

EFECTUL RULARII:
crearea stivei
nr de elemente in stiva = 2
informatia utila= 1
informatia utila= 2
LISTARE in ordine inversa introducerii in stiva
21 cautarea in stiva key= 1
cheia de cautare e gasita pe pozitia 0
extragerea din stiva 2

Process returned 0 (0x0) execution time : 5.005 s
Press any key to continue.

TEMA:

-se cere ca stiva sa aiba doar elemente cuprinse intre 0 si 10.

-se cere ca listarea stivei sa se faca intr-un fisier extern(urmariti operatiile cu fisiere de la clasa a 10-a)

Coada

este un caz particular de lista la care extragerea se face la un capat si la celalalt capat se adauga noile elemente . Se modeleaza un caz real - cel al cozii la magazin , la o casa de bilete etc

Cine e la inceput e procesat si pleaca din coada , cine vine nou in coadă stă pana ce ii vine randul !

Exista insa si cozi cu prioritati - unde se poate da prioritate unui element pentru procesare.

Alt exemplu : queue print job-ul - coada de listare la imprimanta de retea .

COADA IN ALOCARE STATICA -foloseste doi indici FRONT si REAR

using namespace std;
int queue[100],front,rear,n,i,j,info,key;
int main()
{
cout << "crearea cozii" << endl;
front=-1;rear=-1;//
cout<<"nr de elemente in coada = "; cin>>n;
for(i=0;i<n;i++) {
cout<<"informatia utila= "; cin>>info;
if(front==-1) {front=0;rear=0;queue[rear]=info;}
else {rear++;queue[rear]=info;}
}
cout<<"LISTARE coada "<<endl;
for(i=0;i<n;i++) cout<<queue[i]<<endl;
cout<<" cautarea in coada ";cout<<"key= "; cin>>key;
for(i=n-1;i>-1;i--)if(queue[i]==key)cout<<"cheia de cautare e gasita pe pozitia "<<i<<endl;
cout<<"extragerea din coada ";
cout<<queue[front]<<endl;
return 0;
}
TEMA

inaintea randului final al programului - cel cu return 0 inserati instructiuni ce deplaseaza in coada elementele ramase cu o pozitie , deoarece a fost extras un element
la cautare daca se introduce o cheie ce nu e in coada programul nu returneaza nimic , adaugati o linie de cod care sa dea un mesaj si in aceasta situatie

LISTA

------------------------------------------------------------------------------
STIVA

PROGRAMUL URMATOR ILUSTREAZA OPERATIILE CU LISTE

#include<stdio.h>

#include<conio.h>

struct nod{int inf;

nod* urm;

};

void main()

{int n,i,info,d;

nod* p,*primul,*ultimul,*aux;

printf("dati numarul de elemente al listei n=");scanf("%d",&n);

printf("dati informatia din primul nod info=");scanf("%d",&info);

p=new nod;

p->inf=info;

p->urm=NULL;

primul=p;

ultimul=p;

for(i=2;i<=n;i++)

{printf("dati informatia din nod %d =",i);scanf("%d",&info);

p=new nod;

p->inf=info;

p->urm=NULL;

ultimul->urm=p;

ultimul=p;

}

printf("\n lista initiala este:");

p=primul;

for(i=1;i<=n;i++)

{printf("%d ",p->inf);

p=p->urm;

}

printf("\n unde doriti sa faceti inserarea? Inainte=1, dupa=2----");scanf("%d",&d);

if (d==1)

{printf("dati valoarea din nodul ce va fi adaugat inainte de ultima inregistrare=");

scanf("%d",&info);

p=new nod;

p->inf=info;

aux=primul;

while(aux->urm->urm!=NULL) aux=aux->urm;

p->urm=ultimul;

aux->urm=p;

}

if (d==2)

{printf("dati valoarea din nodul ce va fi adaugata dupa ultima inregistrare=");

scanf("%d",&info);

p=new nod;

p->inf=info;

p->urm=NULL;

ultimul->urm=p;

ultimul=p;

}

printf("\n lista dupa modificari este:");

p=primul;

while(p!=NULL)

{printf("%d ",p->inf);

p=p->urm;

}

getch();

}

PROGRAMUL URMATOR ILUSTREAZA LISTA LINIARA

#include<stdio.h>

#include<conio.h>

struct nod{int inf;

nod* urm;

};

void main()

{int n,i,info;

nod* p,*primul,*ultimul;

printf("dati numarul de elemente al listei n=");scanf("%d",&n);

printf("dati informatia din primul nod info=");scanf("%d",&info);

p=new nod;

p->inf=info;

p->urm=NULL;

primul=p;

ultimul=p;

for(i=2;i<=n;i++)

{printf("dati informatia din nod %d =",i);scanf("%d",&info);

p=new nod;

p->inf=info;

p->urm=NULL;

ultimul->urm=p;

ultimul=p;

}

p=primul;

for(i=1;i<=n;i++)

{printf("%d ",p->inf);

p=p->urm;

}

getch();

}

LISTELE CIRCULARE SUNT MODELATE PRIN PROGRAMUL URMATOR

#include<iostream.h>

#include<conio.h>

struct Nod

{int info;

Nod *next,*back;};

Nod *prim, *ultim;

int n;

void creare_lista()

{Nod *c;

c=new Nod;

cout<<"info ";

cin>>c->info;

if(!prim)

{prim=c;

prim->next=0;

prim->back=0;

ultim=prim;

}

else

{ultim->next=c;

c->back=ultim;

ultim=c;

ultim->next=0;

}

void listare_stanga_dreapta()

{Nod *c;

c=prim;

while(c)

{cout<<c->info<<" ";

c=c->next;}

}

void creaza_lista_circulara()

{ultim->next=prim;

prim->back=ultim;

}

void afiseaza_lista_circulara(Nod *c) //se parcurge lista pornind de la o adresa transmisa

{for(int i=1;i<=n;i++)

{cout<<c->info<<" ";

c=c->next;}

}

void main()

{int i;

clrscr();

cout<<"cate elemente va avea lista?";

cin>>n;

for(i=1;i<=n;i++)

creare_lista();

cout<<endl<<"Elementele listei de la stanga la dreapta sunt:"<<endl;

listare_stanga_dreapta();

creaza_lista_circulara();

cout<<endl<<"afiseaza lista circulara incepand de la primul :"<<endl;

afiseaza_lista_circulara(prim);

cout<<endl<<"afiseaza lista circulara incepand de la al doilea :"<<endl;

afiseaza_lista_circulara(prim->next);

cout<<endl<<"afiseaza lista circulara incepand de la ultimul :"<<endl;

afiseaza_lista_circulara(ultim);

getch();

}

TESTARE SI NOTARE

pt nota 1
activitatea de laborator
pt nota 2
a) Se scriu in caiet programele pt lista , lista circulara . (blog)
b)Definitii stiva , lista , coada .(caiet)
c)se cere un program pe o coala semnat in care sa aveti o lista cu abonati ai unei firme de comunicatii telefonice (INDICATIE -se adapteaza informatia utila la crearea cu instructiunea STRUCT a structurii generice a unui nod ; practic aveti mai sus exemplele , ele trebuind doar sa fie adaptate ; de pilda punem in struct char[20] nume ; char[20] prenume ; char[11] nr-tel ; adaptarea programului presupune adaugarea unor instructiuni pt aceste campuri )

Grafuri

Sunt formate din doua mulțimi - V mulțimea de vârfuri și U mulțimea de muchii G=(V,U) e notația convențională
Grafurile orientate sunt numite și digrafuri
Muchiile la graful orientat de numesc arce.
Un lanț L de extremități x și y este format dintr-o înșiruire de vârfuri legate între ele prin muchii care incep cu vârful x și se termina cu y

Drumul D de extremități x și y este de fapt un lanț în cazul unui graf orientat.Conexitatea este acea proprietate prin care un graf are posibilitatea de a interconecta orice vârf x cu orice alt vârf y al său
Reprezentarea cea mai uzuala de face prin matricea de adiacenta A .
Matricea extinsă de adiacentă este A barat și ne arata daca există sau nu lanț între nodul i și nodul j pt orice i și j din mulțimea V.

G este eulerian daca contine un ciclu eulerian in care orice muchie apare o singura data .
G este graf hamiltonian daca si numai daca contine un ciclu hamiltonian in care orice varf apare o singura data .

daca un graf e conex atunci matricea de adaiacenta extinsa are numai valori de 1

Teor. Un graf este eulerian daca si numai daca este conex si are pentru orice varf grad par .

//g este eulerian?

#include<stdio.h>

#include<conio.h>

#include<iostream.h>

int n,i,j,k,s,a[10][10];

void citire()

{

cout<<"n=";

cin>>n;

for(i=1;i<=n;i++)

for(j=1;j<=n;j++)

{

cout<<"a["<<i<<j<<"]=";

cin>>a[i][j];

}

int conex()

{

int t;

t=1;

for (i=1;i<=n;i++)

for(j=1;j<=n;j++)

for(k=1;k<=n;k++)

if ((a[i][j]==0)&&(a[i][k]==1)&&(a[k][j]==1)&&(i!=j)&&(j!=k)&&(i!=k)) a[i][j]=1;

for (i=1;i<=n;i++) for(j=1;j<=n;j++) if((a[i][j]==0)&&(i!=j)) t=0;

return t;

}

int par()

{

int p=1,d;

for (i=1;i<=n;i++)

{

d=0;

for(j=1;j<=n;j++)

d=d+a[i][j];

if (d%2!=0)p=0;

}

return p;

}

void main()

{

citire();

if( par && conex) cout<<"g eulerian";

else cout<<"g nu e eulerian" ;

getch();

}

Teorema. Un graf G este hamiltonian daca si numai daca este conex si are gradele varfurilor de grade d(x) >= n/2.

//g este hamiltonian ?
#include<stdio.h>
#include<conio.h>
#include<iostream.h>
int n,i,j,k,s,a[10][10];
void citire()
{
cout<<"n=";
cin>>n;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
cout<<"a["<<i<<j<<"]=";
cin>>a[i][j];
}
}

int grad()
{
int p=1,d;
for (i=1;i<=n;i++)
{
d=0;
for(j=1;j<=n;j++)
d=d+a[i][j];
if (d<n/2)p=0;
}
return p;
}
void main()
{
citire();
if( grad()) cout<<"g hamiltonian";
else cout<<"g nu e hamiltonian" ;
getch();
}

APLICAȚIE

Matricea de adiacenta
#include<fstream.h>
int a[10][10],n,m,i,j;
ifstream f("in.txt");
ofstream g("out.txt");
void citire()
{
f>>n;
for(i=0;i<n;i++) for(j=0;j<n;j++) f>>a[i][j];
}

//TEMA pt nota -afisarea linie cu linie a matr de adiac in fisierul out.txt
//programul principal main cu apelul functiilor citire si afisare

PARCURGEREA GRAFURILOR NEORIENTATE se aplica si la cazul particular al arborilor .
parcurgerea DF si BF

Grafuri orientate

Verificare :

Def. grafurile orientate(digrafurile).
Ce propr. nu au comparativ cu cele neorientate .
Cum se parcurg grafurile ?
Cum se reprezinta grafurile?
Def. Grafuri euleriene , hamiltoniene.Definitii. Propoz. Matematice.
Precizati ce rol are metoda backtracking in informatica .
Scrieti alg. Df in 5 min. cu caietul si cartea inchise.
Scrieti alg BF in aceleasi conditii in 5 min.

Se noteaza toti elevii .

3p din of.

Similar notiunii de lant avem notiunea de drum .

Arcul e similar notiunii de muchie.

Matricea de adiacenta nu mai are proprietatea de simetrie pentru orice graf.

Totusi diagonala principala are numai valori de 0 .

Reprezentarea se face de regula prin matrice de de adiacenta ,matricea de incidenta , matricea costurilor, lista de adiacente numita si lista de vecinatati .

O problema de mare importanta a fost aceea de a determina daca exista drumuri intre varfurile grafului. Matricea existentei drumurilor este construita cu codul sursa utilizat la construirea matricei extinse care a fost prezentata la conexitatea grafurilor.

Pentru grafuri ponderate, ce au asociate muchiilor numere reale(costuri) o problema este aceea de a gasi pentru 2 varfuri oarecare i si j “drumul de cost minim”. Aceasta problema a gasirii costurilor minime se materializeaza la un graf intreg in asa numita creare a arborelui de cost minim (acesta contine adesea mai putine muchii – e practic un graf partial).

Costul minim se obtine pentru un drum care are suma de costuri mai mica decat a

altor drumuri.

Ex. Putem ajunge de la vf. 1 la varful 5 parcurgand muchii cu costuri pe care le insumam asa 5+3+1 sau asa 10+2+3+5. Deci muchiile(3 muchii) din primul drum se selecteaza pentru drumul de cost minim.

Algoritmul de mai jos gaseste costurile minime pentru toate perechiile de varfuri i si j oarecare

Pas 1 citim n-nr. de varfuri , citim matricea de adiacenta ,citim i si j

Pas2 pentru i de la 1 la n

pentru j de la 1 la n

pentru k de la 1 la n

daca c[i,j] >c[i,k]+c[k,j] atunci c[i,j]=c[i,k]+c[k,j]

ARBORI

Cand vorbim de arbori notiunea de varf e inlocuita de notiunea de nod .

Def. Numim arbore un graf conex si fara cicluri

Def. Un arbore este un graf aciclic pentru care exista un nod numit radacina si orice 2 noduri i si j exista un drum prin radacina care le uneste .

Nodurile fara descendenti se numesc noduri terminale sau frunze.

Nodurile se reprezinta pe nivele . Nodurile ce deriva dintr-un nod aflat pe un nivel superior se numesc descendenti sau chiar fii ai nodului in cauza.

Avem notiuni de fiu,frate,parinte, descendent.

Un arbore nu are niciodata varfuri izolate.

Propozitie:

Urmatoarele afirmatii sunt echivalente :

1.G este arbore

2.G conex si aciclic

3.G are m=n-1 muchii si e conex

4.G e aciclic si are m=n-1 muchii

TEST combinat(practic si scris)

IMAGINE CU -->GRAFUL

LUCRARE

1.Se scrie in caiet matricea de adiacenta pt graful de la proiector .

2.Se ruleaza in C++ un program de parcurgere

( depth first sau breadth first) in blog .....la grafuri

3.Graful este conex ? Motivam in scris

4.Graful este complet ? Motivare in scris

5.Graful este arbore ? Motivati.

Pentru un graf ponderat algoritmul de mai jos construieste arborele de cost minim

C2=multimea vida

Pas1 Se considera o partitie T1={1},T2={2},...,Tn ={n} a multimii varfurilor .

Se ordoneaza muchiile dupa costuri C1={c1,c2,.....,cn}.

Se alege prima muchie din multimea C1 (elementele se verifica prin sondaj de la stanga la dreapta) care nu are ambele extremitati in T1.

Se extrage aceasta muchie din multimea C1.

Se adauga muchia in multimea C2.

Varful ce e extremitate a muchiei si nu apartine lui T1 se plaseaza in T1.

Pas 2 Se repeta pasul 1 pana cand T1=V, unde V e multimea varfurilor grafului.

Pas 3 Se afiseaza arborele de cost minim {T1,C2}

Observatie : arborele de cost minim e un graf partial , totusi structural el este in acelasi timp un arbore.

Tema de referat : realizati un program pentru construirea arborelui de cost minim

Arborii binari sunt utilizati pt reprezentarea unor expresii matematice , pt a explica diverse probleme.

Capitolul acesta e utilizat in proiectarea procesoarelor , in analize lexicale , gramaticale , în chestiuni legate de crearea si administrarea motoarelor de vorbire (speach engine) , dezvoltarea legăturilor asociative în inteligența artificială.

Operatiile de parcurgere a arborilor binari se simplifica mult daca vom considera ca fiecare nod al arborelui subordoneaza un subarbore binar stang si un subarbore binar drept. Avand in vedere aceasta observatie se vor defini subprograme recursive care utilizeaza tehnica Divide et Impera.

Principalele modalitati de parcurgere ale unui arbore binar sunt:

A) Arborii binari pot fi parcursi prin metode specifice grafurilor: in adancime, latime.

B) Metode specifice arborilor binari :

Parcurgerea in inordine (stanga –varf – dreapta SVD) – se parcurge mai intai subarborele stang, apoi varful, apoi subarborele drept.
Parcurgerea in preordine (varf- stanga – dreapta VSD) – se parcurge mai intai varful, apoi subarborele stang, apoi subarborele drept.
Parcurgerea in postordine (stanga – dreapta – varf SDV) – se parcurge mai intai subarborele stang, apoi subarborele drept si la sfarsit varful.

Solutiile de parcurgere ale arborelui din figura urmatoare :

TEST

1.Incercati sa desenati arborele asociat acestor parcurgeri .
2.Construiti vectorul de tati asociat
T=(..................)
3.

parcurgere srd - in inordine

4 2 5 1 6 3 7 8

parcurgere rsd - in preordine

1 2 4 5 3 6 7 8

parcurgere sdr - in postordine

4 5 2 6 8 7 3 1

Programul urmator genereaza un arbore binar memorat in heap si il parcurge prin cele 3 metode.

#include<iostream.h>

#include<conio.h>

struct nod{int nro;

nod*st,*dr;};

nod *r;

void svd(nod *c)

{if(c)

{svd(c->st);

cout<<c->nro<<" ";

svd(c->dr);

}

void vsd(nod *c)

{if(c)

{cout<<c->nro<<" ";

vsd(c->st);

vsd(c->dr);

}

void sdv(nod *c)

{if(c)

{sdv(c->st);

sdv(c->dr);

cout<<c->nro<<" "; }

nod* citire_h()

{int nr;

nod*c;

cout<<"nr de ordine ";

cin>>nr;

if(nr)

{c=new nod;

c->nro=nr;

c->st=citire_h();

c->dr=citire_h();

return c;

}

else

return 0;

}

void main()

{clrscr();

r=citire_h();

cout<<endl<<"parcurgere svd - in inordine "<<endl;

svd(r);

cout<<endl<<"parcurgere vsd - in preordine "<<endl;

vsd(r);

cout<<endl<<"parcurgere sdv - in postordine "<<endl;

sdv(r);

getch();

}

Se numeste arbore de cautare un arbore binar ale carui noduri au o cheie de identificare, iar pentru fiecare nod sunt valabile proprietatile urmatoare:

Orice cheie asociata unui nod este mai mare decat cheia subordonatului stang
Orice cheie asociata unui nod este mai mica decat cheia subordonatului drept

Cheile de identificare sunt distincte.

Fie arborele din figura urmatoare. Cheile sunt : 30, 21 , 27, 15, 37, 31, 33, 36, 35, 24

Observatie: ordinea de inserare a cheilor poate determina o alta configuratie pentru arbore. Spre exemplu daca se insereaza mai intai 30 si apoi 27 si 21 atunci 27 va deveni subordonat stang pentru 30 si 21 subordonat stang pentru 27.

Crearea arborilor de cautare se realizeaza aplicand de un numar de ori operatia de inserare. Inserarea se realizeaza astfel:

-se compara valoarea k de inserat cu cheia asociata nodului curent. Exista urmatoarele posibilitati:

- cheia coincide cu valoarea de inserat si se renunta la inserare

- cheia este mai mica decat k caz in care se incearca inserarea in subarborele drept

- cheia este mai mare decat k caz in care se incearca inserarea in subarborele stang

- inserarea propriuzisa se realizeaza atunci candsubarborele stang , respectiv drept, este vid, altfel se reia.

Parcurgerea arborilor de cautare se face ca orice arbore binar (svd, vsd sdv).

Cautarea unei valori se determina in mod similar cu subprogramul de inserare.

#include<iostream.h>

#include<conio.h>

struct nod

{int nr_o;

nod*st,*dr;

};

nod *v;

int n,k;

void inserare(nod *&c,int k)

{if(c)

if(c->nr_o==k)

cout<<"nr deja inserat "<<endl;

else

if(c->nr_o<k)

inserare(c->dr,k);

else

inserare(c->st,k);

else

{c=new nod;

c->nr_o=k;

c->st=c->dr=0;}

}

void svd(nod *c) //parcurgere in inordine

{if(c)

{svd(c->st);

cout<<c->nr_o<<" ";

svd(c->dr);

}

int cautare(nod *c,int k)

{if(c)

if(c->nr_o==k)

return 1;

else

if(c->nr_o<k)

cautare(c->dr,k);

else

cautare(c->st,k);

else

return 0;

}

void main()

{//v=0;

cout<<"nr de noduri ";

cin>>n;

for(int i=1;i<=n;i++)

{cout<<"valoarea de inserat ";

cin>>k;

inserare(v,k);}

cout<<endl<<"arborele are urmatoarele noduri "<<endl;

svd(v);

cout<<endl<<"valoarea de cautat ";

cin>>k;

if(cautare(v,k))

cout<<"s-a gasit!";

else

cout<<"nu s-a gasit!";

getch();

}

Dupa stergere arborele trebuie sa ramana de cautare.

Fie valoarea 80 a nodului care urmeaza a fi sters. Intervin urmatoarele situatii:

1. nodul care urmeaza a fi sters este nod terminal caz in care se face stergerea (se elibereaza zona de memorie si adresa se inlocuieste cu 0) ceea ce inseamna ca parintele acestuia va avea adresa catre el inlocuita cu 0.

Rezulta:

2. nodul care urmeaza a fi sters subordoneaza un singur subarbore, cel drept, caz in care parintelui sau i se va inlocui adresa catre el cu adresa subarborelui drept respectiv

Rezulta:

3. nodul care urmeaza a fi sters subordoneaza un singur subarbore, cel stang, caz in care parintelui sau i se va inlocui adresa catre el cu adresa subarborelui stang respectiv

4. nodul care urmeaza a fi sters subordoneaza doi subarbori caz in care se procedeaza astfel:

„in locul” informatiei nodului sters va trece cea mai mare valoare din subarborele sau stang.

Aceasta valoare se gaseste la cel mai din dreapta nod din subarborele stang.

Fie acest nod *f. Fiind cel mai din dreapta inseamna ca acesta va subordona cel mult un subarbore stang. Adresa acestui subarbore „va trece in locul” lui f.

o solutie de implementare este:

void cmd(nod* &c,nod* &f)

{nod *aux;

if(f->dr)

cmd(c,f->dr);

else

{c->nr_o=f->nr_o;

aux=f;

f=f->st;

delete aux;

}

void sterg(nod *&c,int k)

{nod *aux,*f;

if(c)

if(c->nr_o==k)

if(c->st==0&&c->dr==0) //daca e nod terminal

{delete c;

c=0;

}

else

if(c->st==0) //are numai subordonat drept

{aux=c->dr;

delete c;

c=aux;}

else

if(c->dr==0) //are numai subordonat drept

{aux=c->st;

delete c;

c=aux;}

else

cmd(c,c->st); //are ambii subordonati

else

if(c->nr_o<k)

sterg(c->dr,k);

else

sterg(c->st,k);

else

cout<<"valoarea de sters nu se gaseste in arbore ";

}

void main()

{int i,n,a;

cout<<"nr. de noduri ";

cin>>n;

for(i=1;i<=n;i++)

{cout<<"valoarea de inserat ";

cin>>a;

inserare(v,a);

}

cout<<endl<<"arborele contine urmatoarele noduri "<<endl;

svd(v);

cout<<endl<<"valoarea de sters ";

cin>>a;

sterg(v,a);

cout<<endl<<"arborele contine dupa stergere urmatoarele noduri "<<endl;

svd(v);

getch();

}

Programul de mai jos implementeaza un arbore partial de cost minim :

#include<fstream.h>

#include<values.h>

#include<conio.h>

int n,m,v,s[20],t[20];

long int a[20][20],min;

const long int infinit=MAXLONG;

void citire()

{int i,j,x,y,z;

fstream f;

f.open("arbminim.txt",ios::in);

if(f)

cout<<"ok"<<endl;

else cout<<"error!!";

f>>n>>m;

for(i=1;i<=n;i++)

for(j=1;j<=n;j++)

{if(i==j)

a[i][j]=0;

else

a[i][j]=infinit;

}

for(i=1;i<=m;i++)

{f>>x>>y>>z;

a[x][y]=a[y][x]=z;}

}

int cauta_nod(int &nod)

{ min=infinit;

for(int i=1;i<=n;i++)

if(s[i]!=0)

if(a[i][s[i]]<min)

{min=a[i][s[i]];

nod=i;}

return min;

}

void actualizeaza(int nod)

{for(int i=1;i<=n;i++)

if(s[i])

if(a[i][s[i]]>a[i][nod])

s[i]=nod;

}

void main()

{ int k,i,j,cost=0;

clrscr();

citire();

cout<<"nodul de inceput ";

cin>>v;

s[v]=0;

for(i=1;i<=n;i++)

if(i!=v)

s[i]=v;

int nod;

for(k=1;k<=n-1;k++)

{min=cauta_nod(nod);

t[nod]=s[nod];

cost=cost+min;

s[nod]=0;

actualizeaza(nod);

}

cout<<"costul este "<<cost<<endl;

cout<<"arborele de cost minimal ";

for(i=1;i<=n;i++)

cout<<t[i]<<" ";

getch();

}

GRAFURILE si ARBORII se pot parcurge cu urmatoarele programe :

TEST
INLOCUITI COADA cu o stiva si realizati parcurgerea in adancime !

TEST E posibil sa ruleze pe un server node.js
Creati 3 grafuri neorientate complete K3,K4,K5

<!DOCTYPE html>
<html>
<head>
<meta name="viewport" content="width=device-width, initial-scale=1">
<title>State Chart</title>
<meta name="description" content="A finite state machine chart with editable and interactive features." />

<meta charset="UTF-8">
<script src="go.js"></script>
<script src="goSamples.js"></script> 
<script id="code">
function init() {
if (window.goSamples) goSamples(); // init for these samples -- you don't need to call this
var $ = go.GraphObject.make; // for conciseness in defining templates
myDiagram =
$(go.Diagram, "myDiagramDiv", // must name or refer to the DIV HTML element
{
// start everything in the middle of the viewport
initialContentAlignment: go.Spot.Center,
// have mouse wheel events zoom in and out instead of scroll up and down
"toolManager.mouseWheelBehavior": go.ToolManager.WheelZoom,
// support double-click in background creating a new node
"clickCreatingTool.archetypeNodeData": { text: "new node" },
// enable undo & redo
"undoManager.isEnabled": true
});
// when the document is modified, add a "*" to the title and enable the "Save" button
myDiagram.addDiagramListener("Modified", function(e) {
var button = document.getElementById("SaveButton");
if (button) button.disabled = !myDiagram.isModified;
var idx = document.title.indexOf("*");
if (myDiagram.isModified) {
if (idx < 0) document.title += "*";
} else {
if (idx >= 0) document.title = document.title.substr(0, idx);
}
});
// define the Node template
myDiagram.nodeTemplate =
$(go.Node, "Auto",
new go.Binding("location", "loc", go.Point.parse).makeTwoWay(go.Point.stringify),
// define the node's outer shape, which will surround the TextBlock
$(go.Shape, "RoundedRectangle",
{
parameter1: 20, // the corner has a large radius
fill: $(go.Brush, "Linear", { 0: "rgb(254, 201, 0)", 1: "rgb(254, 162, 0)" }),
stroke: null,
portId: "", // this Shape is the Node's port, not the whole Node
fromLinkable: true, fromLinkableSelfNode: true, fromLinkableDuplicates: true,
toLinkable: true, toLinkableSelfNode: true, toLinkableDuplicates: true,
cursor: "pointer"
}),
$(go.TextBlock,
{
font: "bold 11pt helvetica, bold arial, sans-serif",
editable: true // editing the text automatically updates the model data
},
new go.Binding("text").makeTwoWay())
);
// unlike the normal selection Adornment, this one includes a Button
myDiagram.nodeTemplate.selectionAdornmentTemplate =
$(go.Adornment, "Spot",
$(go.Panel, "Auto",
$(go.Shape, { fill: null, stroke: "blue", strokeWidth: 2 }),
$(go.Placeholder) // a Placeholder sizes itself to the selected Node
),
// the button to create a "next" node, at the top-right corner
$("Button",
{
alignment: go.Spot.TopRight,
click: addNodeAndLink // this function is defined below
},
$(go.Shape, "PlusLine", { width: 6, height: 6 })
) // end button
); // end Adornment
// clicking the button inserts a new node to the right of the selected node,
// and adds a link to that new node
function addNodeAndLink(e, obj) {
var adornment = obj.part;
var diagram = e.diagram;
diagram.startTransaction("Add State");
// get the node data for which the user clicked the button
var fromNode = adornment.adornedPart;
var fromData = fromNode.data;
// create a new "State" data object, positioned off to the right of the adorned Node
var toData = { text: "new" };
var p = fromNode.location.copy();
p.x += 200;
toData.loc = go.Point.stringify(p); // the "loc" property is a string, not a Point object
// add the new node data to the model
var model = diagram.model;
model.addNodeData(toData);
// create a link data from the old node data to the new node data
var linkdata = {
from: model.getKeyForNodeData(fromData), // or just: fromData.id
to: model.getKeyForNodeData(toData),
text: "transition"
};
// and add the link data to the model
model.addLinkData(linkdata);
// select the new Node
var newnode = diagram.findNodeForData(toData);
diagram.select(newnode);
diagram.commitTransaction("Add State");
// if the new node is off-screen, scroll the diagram to show the new node
diagram.scrollToRect(newnode.actualBounds);
}
// replace the default Link template in the linkTemplateMap
myDiagram.linkTemplate =
$(go.Link, // the whole link panel
{
curve: go.Link.Bezier, adjusting: go.Link.Stretch,
reshapable: true, relinkableFrom: true, relinkableTo: true,
toShortLength: 3
},
new go.Binding("points").makeTwoWay(),
new go.Binding("curviness"),
$(go.Shape, // the link shape
{ strokeWidth: 1.5 }),
$(go.Shape, // the arrowhead
{ toArrow: "standard", stroke: null }),
$(go.Panel, "Auto",
$(go.Shape, // the label background, which becomes transparent around the edges
{
fill: $(go.Brush, "Radial",
{ 0: "rgb(240, 240, 240)", 0.3: "rgb(240, 240, 240)", 1: "rgba(240, 240, 240, 0)" }),
stroke: null
}),
$(go.TextBlock, "transition", // the label text
{
textAlign: "center",
font: "9pt helvetica, arial, sans-serif",
margin: 4,
editable: true // enable in-place editing
},
// editing the text automatically updates the model data
new go.Binding("text").makeTwoWay())
)
);
// read in the JSON data from the "mySavedModel" element
load();
}
// Show the diagram's model in JSON format
function save() {
document.getElementById("mySavedModel").value = myDiagram.model.toJson();
}
function load() {
myDiagram.model = go.Model.fromJson(document.getElementById("mySavedModel").value);
}
</script>
</head>
<body onload="init()">
<div id="sample">
<div id="myDiagramDiv" style="border: solid 1px black; width: 100%; height: 400px"></div>

<p>
The Button's <a>GraphObject.click</a> method creates a new node data,
adds it to the model, and creates a link from the original node data to the new node data.
All of this is done inside a transaction, so that it can be undone by the user
(Ctrl+Z and Ctrl+Y will undo and redo transactions). After the node is created,
<a>Diagram.scrollToRect</a> is called in case it is off-screen.
</p>
<div>
<div>
<button id="SaveButton" onclick="save()">Save</button>
<button onclick="load()">Load</button>
Diagram Model saved in JSON format:
</div>
<textarea id="mySavedModel" style="width:100%;height:300px">
{ "nodeKeyProperty": "id",
"nodeDataArray": [
{ "id": 0, "loc": "120 120", "text": "Initial" },
{ "id": 1, "loc": "330 120", "text": "First down" },
{ "id": 2, "loc": "226 376", "text": "First up" },
{ "id": 3, "loc": "60 276", "text": "Second down" },
{ "id": 4, "loc": "226 226", "text": "Wait" }
],
"linkDataArray": [
{ "from": 0, "to": 0, "text": "up or timer", "curviness": -20 },
{ "from": 0, "to": 1, "text": "down", "curviness": 20 },
{ "from": 1, "to": 0, "text": "up (moved)\nPOST", "curviness": 20 },
{ "from": 1, "to": 1, "text": "down", "curviness": -20 },
{ "from": 1, "to": 2, "text": "up (no move)" },
{ "from": 1, "to": 4, "text": "timer" },
{ "from": 2, "to": 0, "text": "timer\nPOST" },
{ "from": 2, "to": 3, "text": "down" },
{ "from": 3, "to": 0, "text": "up\nPOST\n(dblclick\nif no move)" },
{ "from": 3, "to": 3, "text": "down or timer", "curviness": 20 },
{ "from": 4, "to": 0, "text": "up\nPOST" },
{ "from": 4, "to": 4, "text": "down" }
]
}
</textarea>
</div>
</div>
</body>

</html>

Pagini

[Liste / stive/cozi/ grafuri /arbori]

Lista

este o structură de date în care elementele sunt de același tip , orice element mai puțin primul are un predecesor și orice element mai puțin ultimul are un succesor.

Stiva

Mai jos vom ilustra o stiva in alocare dinamica . Retinem ca se initializeaza stiva , primul element in stiva este practic si ultimul , se retin doi pointeri relevanti : baza si varful stivei top.

STIVA IN ALOCARE STATICA

Coada

este un caz particular de lista la care extragerea se face la un capat si la celalalt capat se adauga noile elemente . Se modeleaza un caz real - cel al cozii la magazin , la o casa de bilete etc

COADA IN ALOCARE STATICA -foloseste doi indici FRONT si REAR

TESTARE SI NOTARE

Grafuri

APLICAȚIE

ARBORI